Adaptive Multiscale Methods Based on A Posteriori Error Estimates, 2010

Advisor: Jan M. Nordbotten

Short description of the project:

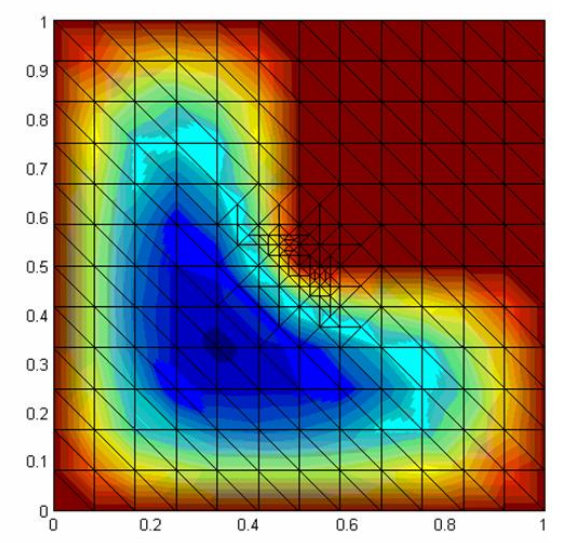
We give an overview of different methods for solving highly heterogeneous elliptic problems with multiscale structure and no intuitive scale separation. We compare different finite element variational multiscale methods and prove the equivalence between the methods proposed by Larson et al. and Nolen et al. We also discuss properties of different multiscale methods depending on the choice of scale separation and ways to represent the fine-scale correction. Additionally, in this work, we give an overview of a posteriori error estimates for the finite element method as well as newly proposed by Larson et al. estimates for the variational multiscale method. As an illustration of the theory, we show our numerical results for using theoretical estimates to construct adaptive algorithms: adaptive refinement of finite elements and adaptive overlap control for variational multiscale methods in the formulation of Nolen et al. There is no known implementation of the latter published at the moment.

Link to thesis at BORA-UiB: https://bora.uib.no/bora-xmlui/handle/1956/13151