Modeling and simulation of blood circulation and perfusion, 2023

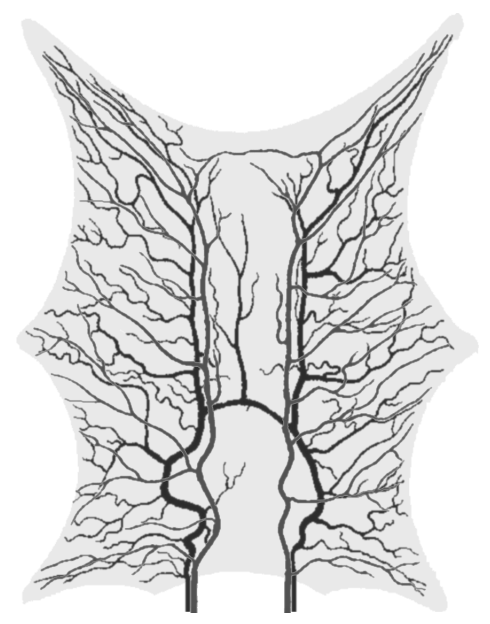
Numerical simulations have become essential for understanding blood circulation and perfusion, as well as providing important insights for medical applications. More realistic models have become possible with technological advances, not only in the form of more complex physics, but also in the flow detail of an entire organ circulation. These characteristics are frequently of interest because blood vessels at different spatial scales have different physiological properties. This thesis focuses on the modeling and simulations of blood flow, tracer transport, and perfusion in an organ tissue. The physical processes are expressed in a multiscale flow model with segmented arteries and veins forming a vascular network flow model that is connected to a microcirculation model. The unobservable vasculature, including small vessels and capillaries, represented by the connection model, is simulated by using a continuum and discrete approach. A multiscale framework for solving blood circulation is presented. The novelty of this framework comes from combining an existing hybrid flow model for a multiscale circulation with vasculature-induced nonlinearities such as vessel wall elasticity and vessel curvature. By using an appropriate linear algebra precondition, the corresponding nonlinear system can be efficiently solved by using an iterative Newton method. This allows us to formulate more realistic blood circulation in a complex physical domain by employing a relatively simple framework with a low computational cost. The models and their implementation are presented in the papers that constitute Part II of this thesis. In the paper section, we propose a framework to generate a digital phantom for perfusion imaging. Moreover, we evaluate tracer kinetic models demonstrating the significant value of post-processing of medical data. We also investigate optimal vascular networks revealing a complex interdependence between the geometry of the vascular network, the capillary bed and organ shape. The results of this thesis contribute to a better understanding of blood perfusion models in tissue and their potential, as well as the potential of scientific computing, for medical applications not limited to perfusion imaging.

Link to the thesis.