Subdivision, simplices and symmetries.

The project is to develop a combinatorial subdivision algorithm from pure mathematics suitable for use in numerical or geometric modelling. Particularly, with a view to problems with important symmetry properties. There are no special qualifications required for this project, but it can be an advantage if one has some training in algebra or topology.

When one wishes to describe a continuous phenomenon with the help of discrete methods, one must be able to divide up the domain into small pieces. There are many methods for doing this, and they each have their advantages and disadvantages. This is particularly demanding if you want to treat phenomena with curves, are of high dimension, or may possess symmetries of one kind or another.

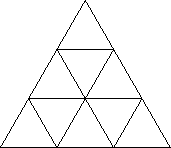
A few years back, a subdivision technique arose in a pure mathematics field that I was engaged in. This technique is called "edgewise subdivision" and has many good properties that are not found in other subdivision techniques. It is based on (higher dimensional) "triangles", and divides these up into smaller "triangles" that each have good properties. In the figure above you see a "3-subdivision" in dimension 2. In dimension 2, the subdivision is very old, but it is only recently that the underlying combinatorics have been understood, such that all the dimensions are equally simple.

Given a body that can be divided up into triangles, edgewise subdivision is a very neat combinatorial technique, which makes it suitable for computer implementation. At the same time, it has a number of good properties. The most exciting property, which I expect may have a wide application potential, is that if the body has a "circular symmetry", then the edgewise subdivision will respect this symmetry. In fact, there are cases where such a subdivision makes the combinatorial coding very much easier.

The thing is, however, that the technique has not yet been explored properly, and I'd like to see that this is done. So far, it is only used in Computer Aided Geometric Design, but I expect that the symmetry property should be able to play an important role in more computation-oriented contexts.

A collaboration with one of the numerical groups would be natural.

References:

[1] Edelsbrunner, H.; Grayson, D. R. Edgewise subdivision of a simplex. ACM Symposium on Computational Geometry (Miami, FL, 1999). Discrete Comput. Geom. 24 (2000), no. 4, 707-719.