Infinite dimensional control on manifolds with boundary

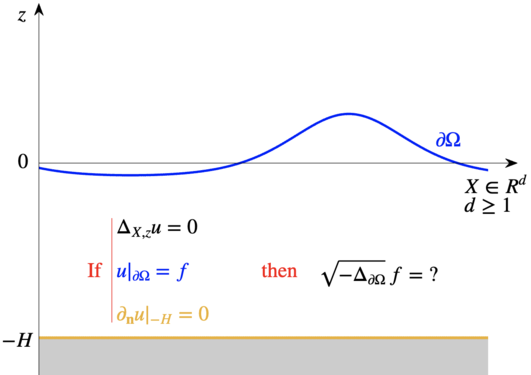
Abstract: The talk will relate to controllability; the ability to reach a certain point in a space given a permissible set of movements.Though there are several standard results for finite-dimensional manifolds, controllability in infinite dimensional spaces are less understood. We are going to focus on the special case of diffeomorphism groups. In 2009, Agrachev and Caponigro described how we could look at how flows of vector fields move points around on a manifold and determine from such observations which diffeomorphisms can be generated by similar flows. We want to consider the same problem, but now allow the manifold to have boundary, and even corners in some special cases. We will both describe the Lie group structure for such groups as well as controllability result. The results presented are based on joint work with Alexander Schmeding (NTNU).