Implementation of an MPFA/MPSA-FV Solver for the Unsaturated Flow in Deformable Porous Media, 2018

Advisors: Jan Martin Nordbotten, Eirik Keilegavlen, Sarah Gasda

Short description of the project:

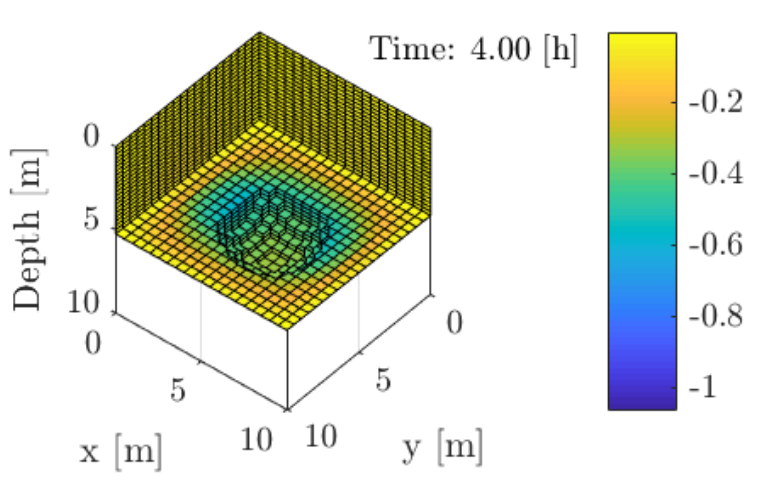
The Unsaturated Flow In Deformable Porous Media (UFIDPM) plays a crucial role in several academic and industrial applications such as; cracks induced by desiccation, collapsing soils, ground movement involving expansive soils, lateral earth surfaces, stability of vertical excavations, natural slopes subjected to environmental changes, construction and operation of a dam, etc. Typically, studying these systems with experimental techniques is impractical. On the other hand, numerical simulations allow us to investigate several scenarios in a short time and with reduced costs. At the moment, only Finite Element Method (FEM) based codes were available. FEM often shows conservative issues and when is applied to UFIDPM instabilities in the limit of incompressibility have been reported. Due to this issues, we were motivated to develop the first Cell-Centered Finite Volume Method (CCFVM) based code for solving UFIDPM. The governing equations are derived following the extended Biot’s theory of three-dimensional consolidation which results in a coupled hydro-mechanical system. For the flow problem, we use the Richards’ equation whereas the mechanical problem is modeled using the linear elasticity equations. For the spatial discretization, we use multi-points approximations schemes. Specifically, Multi Point Flux Approximation (MPFA) for the flow problem and Multi Point Stress Approximation (MPSA) for the mechanical problem. Moreover, the time discretization of the equations was obtained using Backward Euler (BE). The code was implemented in MATLAB R2017b were two core toolboxes (MRST and FV-BIOT) were used. The resulting non-linear set of equations was solved using the Newton method together with Automatic Differentiation (AD). To test the capability of the code several sub-problems were validated. Furthermore, we present a numerical application where we focus on the desiccation process of a clayey soil in a Petri-dish. In this experiment, the water content reduction is caused by instantaneous water evaporation controlled by atmospheric conditions. Finally, by carefully post-processing the resulting stress field, the zones of tensile stress concentration, which corresponds to the areas where cracks are more likely to initiate, are identified.

Link to the thesis at Bora-UiB: https://bora.uib.no/bora-xmlui/handle/1956/17905