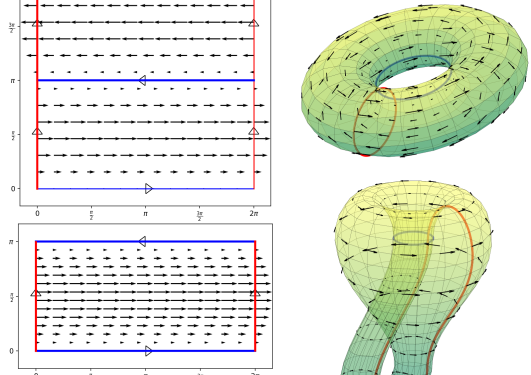
Canonical sub-Riemannian connections
Erlend Grong, Associate Professor @ Department of Mathematics, UiB

Main content
Speaker: Erlend Grong, Associate Professor @ Department of Mathematics, UiB
Abstract:
The topic is sub-Riemannian manifold; manifolds where there we only have inner products defined in some of the directions.
The objective is to be able to determine if two such manifolds are the same, i.e. does or does there not exist an isometry between two different sub-Riemannian manifolds
Similar to the Levi-Civita connection, we discuss a canonical way of defining a Cartan connection on sub-Riemannian manifolds, which gives us a canonical choice of complement and affine connections. We present a new construction, which, unlike the earlier normalization condition of Morimoto, these new connections do not generate extra holonomy when considering general loops compared to horizontal loops.
These results are part of a preliminary work with Jan Slovak. Results are based on a previous work on chain complexes with Francesca Tripaldi.