4. desember: Matematikk og julekorger

Artikkelen om julekorger er skrevet av Gjert-Anders Askevold og publisert i tidskriften TANGENTEN 4/2009.

TANGENTEN er et tidsskrift for matematikkundervisning. 

Gjert-Anders Askevold er høyskolelektor ved seksjonen for matematikk fagdidaktikk, avdeling for lærerutdanning, ved Høyskole i Bergen.

Eg gler meg alltid til desember, då kan eg med godt samvit starte arbeidsdagen med å lage meg ei julekorg. Både som ein fi n start på dei mørke dagene i desember, men og som eit matematisk puslespel. Kollegaene mine ser av og til rart på meg, men og litt spørjande, er dette matematikk?  Eg vil påstå det, og nyttar eitkvart høve til å fl ette det inn i aktivitetar med studentar eller elevar. Kva med å lage seg ein adventskalendar av julekorger, ei korg for kvar dag. Julekorga kan være ei gåve i seg sjølv, eller ein kan gøyme ein liten skatt i julekorga.  Det fyste matematiske området eg tenker på når det gjeld fletting av julekorger, er symmetri, geometriske figurar og problemløysing.  Ser ein litt meir på julekorger, eller aktivitetar rundt dei, kan ein fint flette inn talrekke som fibonaccitala. Julekorger er og ei fin form for etnomatematikk dei fleste kjenner, men ikkje tenkjer over detmatematiske i.  Vidare vil eg ta for meg ulike julekorger og mønster ein kan eksperimentere med i aktivitetar med elevar. Eg har og laga eit dokument med mønster til julekorger, som du kan finne på home.hib.no/ansatte/gaas/Julekorger.pdf. Du kan godt nytte desse til å lage dine eigne julekorger, men mykje av moroa, og det matematiske kjem fram når ein lagar sine eigne mønster.

Mal

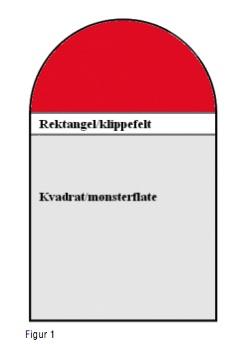
I arbeidet med julekorger kan det vere lurt å ha ein mal (sjå figur 1), som ein nyttar til å lage mønster ut frå, og som ein kan kopiere opp og lage fleire ulike mønster av. Malen er sett saman av eit kvadrat, med ein halvsirkel på eine sida.  Kvadratet skal ein klippeopp i strimlar og flette.  Det er på kvadratet mønsteret (eg kallar det vidare for mønsterflata) kjem fram i den ferdige julekorga. Storleiken på hjartet blir bestemt av kvadratet.  Når ein skal til å klippe opp strimlane ein skal flette, er det svært ofte tenleg å klippe litt opp på halvsirkelen, for å gjere flettinga

lettare.  Eventuelt kan ein «forlengje» kvadratet med eit rektangel, dette er for å gjere strimlane lenger og betre å flette med. (eg kallar rektangelet for klippefelt). Bredda på rektangelet har eg ofte på ca. 1/2 cm.

Papirkvalitet

Ein kan lage julekorger av dei fleste papirtypar, ein kan til og med lage dei av stoff eller filt. Det viktige er at ein har to ulike fargar på papiret, gjerne litt «julete» fargar, som raudt og grønt. Sjølv nyttar eg ofte farga kopipapir. Kopipapir er ofte i A4 storleik, og set ofte litt avgrensingar med omsyn på storleiken av julekorgene. Ein får svært fine korger av glansa papir, som ein kjøper i rullar, men ein kan like godt nytte julegåvepapir. Desse papirtypane kjøper ein ofte i rullar. Før ein skal bruke dei, bør ein ta dei ut av rullane og legge dei under noko tungt, slik at ikkje papiret krøllar seg, og lagar problem når ein skal til å flette korgene.  Når ein har malen (malane) klare, kan ein setje i gang å lage mønster. Dei fyste hjarta ein lagar med elevar kan godt være enkle. Med to eller tre strimlar. Ein vil få fram fi ne symmetriske mønster med desse og, samstundes som ein får arbeida med prinsippet for fletting av julekorger. Når eleven har klart å lage desse, og sett det fine «sjakkmønsteret» ein får fram, kan ein gå i gang med fleire og meir avanserte mønster.

Fletting

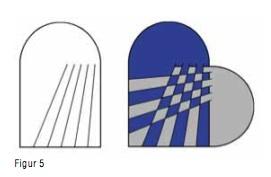
Bruk malen og lag to «doble» flettestykker. Skal flettinga bli ei korg, er bretten vist på teikninga viktig. En treng alltid to flettestykker, i ulikt farga papir. Den enklaste korga å starte med, har to strimlar som vist på figur 2. Når ein flettar plasserar ein dei to bitane, som vist på teikninga og flettar. Prinsippet er: Stikk den første gjennom, den neste trer ein over.

Rette strimlar

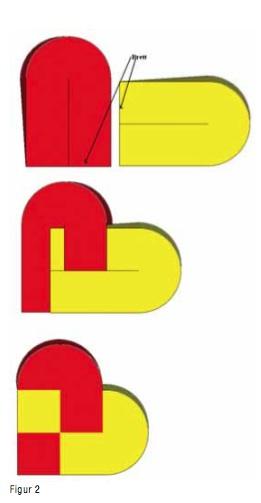
Til no har me arbeida med grunnforma, som er lik i dei fleste julekorger. Me er no klare til å lage fleire og meir avanserte mønster. Å lage mønster, kan gje spanande matematiske utfordringar og utforskingar. Kven kan lage det mest spanande mønsteret? Mønstera kan konstruerast med passar og linjal. Ein kan snakke om halvering, deling i tre, fire osv. Korleis kan ein konstruere det? Delelinjene skal alltid gå frå den neste delen av mønsterflata opp mot halvsirkelen. Teknisk sett er det nok å klippe opp til der rektangelet startar. Men for å gjere flettinga enklare, klipper me opp klippeflata og.  Med like bredder får me ”sjakkmønster” i julekorga. Med ulike bredder på strimlane, kan me få fram endå meir spanande mønster. Eit eksempel kan være julekorga i figur 3. I denne julekorga har strimlane bredde 1:2 i forhold til kvarandre. I tillegg til speilsymmetri, får me og ein fi n rotasjonssymmetri fram i denne korga.  Kva med å nytte fibonaccirekka som inspirasjon til ei julekorg? Fibonaccirekka startar med: 1–1–2–3–5–8–13 … der det neste talet er summen av dei to føregåande. Om me let bredda på strimlane være 1 cm, 1 cm, 2 cm og 3 cm, kan me få fram mønsteret som vist på figur 4.  Legg merke til symmetrien som kjem fram i den ferdige julekorga. Fiboanccirekka er berre ei av mange talrekker, kan ein nytte andre?  

Perspektivisk mønster (anamorft julehjarte)

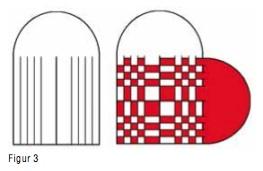
Ved å klippe strimlane på skrå, endrar mønsteret karakter, og blir til eit fordreia sjakkmønster.  Det ferdige mønsteret blir ein projeksjon av «sjakkmønsteret». Ein slik projeksjon blir kalla for ein anamorfose1, som er kjent både i kunsten og i perspektivteikning. Ser me julekorga i figur 5 frå ein bestemt vinkel, vil me sjå sjakkmønsteret slik me vanlegvis ser det. Anamorfe bileter kan ein knytte til

perspektivteikning. Vil du arbeide med, eller lese meir om anamorfe bilete, sjå LAMIS’ Matematikkdagshefte 2010. 

Speilsymmetriske julekorger

Ein siste variant av julekorgmønster eg vil ta med her, er der ein kan få fram symmetriske figurar som englar, juletre, lys osv. Desse ser imponerande ut, men er faktisk enkle å lage.  Ein startar med malen, og teiknar inn diagonalen på mønsterflata. Det er diagonalen som dannar symmetrilinja for mønsteret i den ferdige julekorga.  I fi gur 6 har eg teikna ein halv engel som ligg inntil symmetrilinja. For å kunne klippe ut strimlar til fletting, teiknar (eventuelt konstruerar) eg ei linje frå endepunkta på engelen på diagonalen. Slik blir mønsterflata delt i to «flettestrimlar». Dei heiltrukne linjene i figur 6 er linjene ein skal klippe etter, medan dei grå stipla linjene er hjelpelinjer.  Når ein har klipt etter denne linja, kan ein flette ei korg med ein engel. Vil ein gjere korga litt meir spanande, kan ein klippe mønsterflata opp i fleire strimlar. Når ein skal flette med slike asymmetriske grunnmønster (som ein halv engel), er det viktig å setje dei saman slik at mønsteret kjem rett fram, som vist i figur 7.  Kos deg med julekorgene, og lag deg nye mønster. Kun fantasien set grenser.

Note

1 «En anamorfose er en forvridd projeksjon eller et fortegnet perspektiv, især et bilde som er formet slik at det blir forståelig bare når det blir betraktet på en spesiell måte eller fra et bestemt punkt.» no.wikipedia.org/wiki/Anamorfose, henta 13.10.09